Butler–Volmer equation
The Butler–Volmer equation is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current on an electrode depends on the electrode potential, considering that both a cathodic and an anodic reaction occur on the same electrode:
or in a more compact form:
where:
 : electrode current, A
: electrode current, A : electrode active surface area, m2
: electrode active surface area, m2 : electrode current density, A/m2 (defined as i = I/A)
: electrode current density, A/m2 (defined as i = I/A)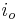 : exchange current density, A/m2
: exchange current density, A/m2 : electrode potential, V
: electrode potential, V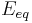 : equilibrium potential, V
: equilibrium potential, V : absolute temperature, K
: absolute temperature, K : number of electrons involved in the electrode reaction
: number of electrons involved in the electrode reaction : Faraday constant
: Faraday constant : universal gas constant
: universal gas constant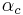 : so-called cathodic charge transfer coefficient, dimensionless
: so-called cathodic charge transfer coefficient, dimensionless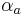 : so-called anodic charge transfer coefficient, dimensionless
: so-called anodic charge transfer coefficient, dimensionless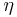 : activation overpotential (defined as
: activation overpotential (defined as 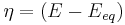 ).
).
The equation is named after chemists John Alfred Valentine Butler and Max Volmer.
Contents |
Mass-transfer control
The previous form of Butler–Volmer equation is valid when the electrode reaction is controlled by electrical charge transfer at the electrode (and not by the mass transfer to or from the electrode surface from or to the bulk electrolyte). Nevertheless, the utility of the Butler–Volmer equation in electrochemistry is wide, and it is often considered to be "central in the phenomenological electrode kinetics".[1]
In the region of the limiting current, when the electrode process is mass-transfer controlled, the value of the current density is:
where:
- D is the diffusion coefficient;
- δ is the diffusion layer thickness;
- C* is the concentration of the electroactive (limiting) species in the bulk of the electrolyte.
The more general form of the Butler–Volmer equation, applicable to the mass transfer-influenced conditions, can be written as:[2]
where:
- i is the current density, A/m2,
- Co and Cr refer to the concentration of the oxidized and the reduced form, respectively,
- C(0,t) is the time-dependent concentration at the distance zero from the surface.
The above form simplifies to the conventional one (shown at the top of the article) when the concentration of the electroactive species at the surface equals to that in the bulk.
The limiting cases
There are two limiting cases of the Butler–Volmer equation:
- the low overpotential region (called "polarization resistance", i.e., when E ≈ Eeq), where the Butler–Volmer equation simplifies to:
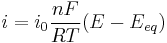 ;
;
- the high overpotential region, where the Butler–Volmer equation simplifies to the Tafel equation:
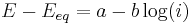 for a cathodic reaction, when E << Eeq, or
for a cathodic reaction, when E << Eeq, or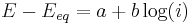 for an anodic reaction, when E >> Eeq
for an anodic reaction, when E >> Eeq
where a and b are constants (for a given reaction and temperature) and are called the Tafel equation constants. The theoretical values of a and b are different for the cathodic and anodic processes.
See also
References
- ^ J. O'M. Bockris, A.K.N.Reddy, and M. Gamboa-Aldeco, "Modern Electrochemistry 2A. Fundamentals of Electrodics.", Second Edition, Kluwer Academic/Plenum Publishers, p.1083, 2000.
- ^ Allen Bard and Larry Faulkner, "Electrochemical Methods. Fundamentals and Applications". 2nd edition, John Wiley and Sons, Inc., 2001.
![I = A \cdot i_0 \cdot \left\{ \exp \left[ \frac { \alpha_a nF } {RT} (E - E_{eq}) \right] - \exp \left[ - { \frac { \alpha_c nF } {RT}} (E - E_{eq}) \right] \right\}](/2012-wikipedia_en_all_nopic_01_2012/I/b13d3c9cd3cdf63f59f3c4d28e069257.png)
![i = i_0 \cdot \left\{ \exp \left[ \frac { \alpha_a nF \eta} {RT} \right] - \exp \left[ - { \frac { \alpha_c nF \eta} {RT}} \right] \right\}](/2012-wikipedia_en_all_nopic_01_2012/I/a77f2485191009658ebc0004687defed.png)
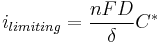
![i = i_0 \left\{ {\frac {C_o(0,t)} {C_o^*}} \exp \left[ \frac { \alpha_a nF \eta} { RT } \right] - {\frac {C_r(0,t)} {C_r^*}} \exp \left[ - { \frac { \alpha_c nF \eta} { RT } } \right] \right\}](/2012-wikipedia_en_all_nopic_01_2012/I/163b2a88fa9470ee3ba325a35cd89900.png)